本文尚未完成,内容还有错误,只当参考资料阅读。
一、问题的提出
有了前面的结论,可以知道电容电压跟随交流电源电压的关系,是满足下面的方程的:
\(V_{C}(t)=\frac{V_{m}}{\sqrt{1+(\omega RC)^2}} \times e^{\frac{-t}{RC}} + \frac{V_{m}}{\sqrt{1+(\omega RC)^2}} \times sin(\omega t-arctan(\omega RC))\)1、这个方程中的 Vm / [(1+(wRC)^2)^(1/2)] 可以被视为A,这个A就是电容电压波形中的峰值。也就是说:在电源正弦的作用下,电容上的电压形成了一个新的正弦波(虽然并不是完整的正弦、起始瞬态略有畸变),这个新形成的“正弦波”的波峰是A;
2、方程中的-arctan(wRC)被视为相移角φ,也就是电容正弦错后于电源正弦的相移;
3、那么新的正弦波的频率呢?频率是不变的。它的频率是和电源频率相同的,只是波峰略低、相位略微向右偏移。
有了如上概念之后,就可以完成以下的两个问题的解答:
1、如何构建一个完美的60°相移,然后通过3组RC相移,完成180°的相移;
2、在进行了180°相移之后的第三组RC网络的输出电压,波峰是多大?也就是说最终反馈回控制极的电压有多少?
这篇博客,将完成上面2个问题的计算和整理。
二、为了实现60°的单组RC相移,重新进行相关元件的参数设置
电源电压峰值:12V。之所以要将电源电压定义为12V,目的是与Jack Kilby的实验相符。在我阅读的相关书籍中提到,他在实验室中用12V直流电开始实验,并在示波器上看到了令人激动的振荡波型;
电源频率:暂定100Hz。之所以要定义成100Hz,是为了方便绘图观察。后期可以重新调整这个频率;
电容:1uF,也就是0.000001F;
电阻:之前我在仿真中是直接使用的1000Ω,现在按照相移角为60°进行计算,电阻应该使用2760Ω。这里还有一个额外的问题:为什么之前仿真中,电容使用1kΩ也可以正常振荡呢?这个问题需要以后有时间了,再深入推敲一下;
如上的基本参数就定义好了,按照上面定义的参数,进行绘图,然后进行仿真,看绘图计算结果与仿真结果是否一致。
三、三组RC相移之后的最终波形及电压
其实有了上面的计算依据之后,不画图也可以计算出经过3次RC相移之后的最终输出电压峰值是多大了。因为经过一组RC之后的电压峰值是A,所以经过3组RC之后的电压峰值是A的三次方。因而,如果电源电压的峰值时12V,那么:
经过第一组RC之后的电压将会是6V左右;第二组RC之后的电压将是3V;第三组之后的电压将是1.5V。也就是说最终反馈回控制极的电压的波动将在+1.5V ~ -1.5V之间。
下面是使用SageMath完成的画图,从只有电源电压开始、一条条的增加新的电容电压曲线。需要注意的是要忽略掉曲线开始瞬态部分的失真情况:
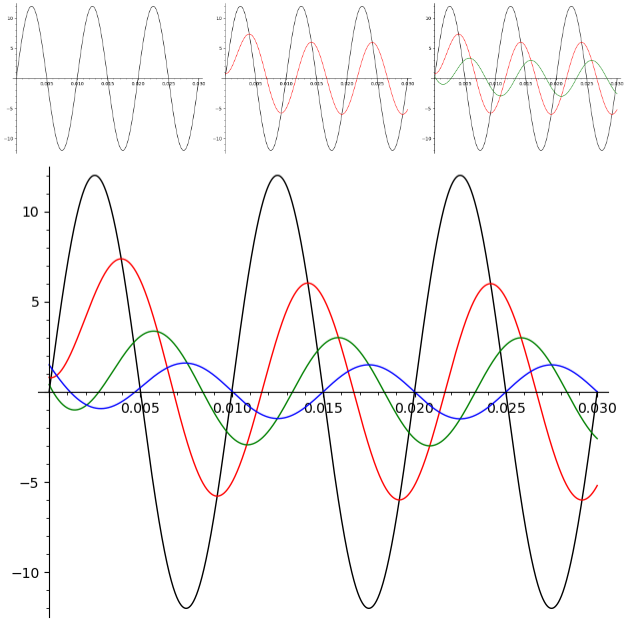
这个开始部分的失真真令人苦恼!要知道我之所以花了很多时间《搞清楚电容电压跟随电源电压的数学公式和推导过程》,目的就是想在最终的SageMath生成准确正确的图像。而现在看来还是无法生成出正确的图像来。
很奇怪各类仿真软件在这里是怎么做的,为什么通过仿真软件的示波器,就能够看到正确的波形图呢?
四、仿真对比
待续
五、备忘
1、本文中使用到的LaTex公式,为了方便日后使用,源码备注如下:
V_{C}(t)=
\frac{V_{m}}{\sqrt{1+(\omega RC)^2}}
\times
e^{\frac{-t}{RC}}
+
\frac{V_{m}}{\sqrt{1+(\omega RC)^2}}
\times
sin(\omega t-arctan(\omega RC))2、本文中使用到的SageMath绘图语句,整理如下,方便日后使用:
Vm = 12
R = 2760
C = 0.000001
F = 100
omega = 2*pi*F
Vs(t) = Vm*sin(omega*t)
A = Vm / sqrt(1+(omega*R*C)^2)
Vc1(t) = A * exp(-t/(R*C)) + A * sin(omega*t-arctan(omega*R*C))
B = A / sqrt(1+(omega*R*C)^2)
Vc2(t) = B * exp(-t/(R*C)) + B * sin(omega*t-arctan(omega*R*C)*2)
CC = B / sqrt(1+(omega*R*C)^2)
Vc3(t) = CC * exp(-t/(R*C)) + CC * sin(omega*t-arctan(omega*R*C)*3)
plot(Vs, 0, 0.03, color='black')
+ plot(Vc1, 0, 0.03, color='red')
+ plot(Vc2, 0, 0.03, color='green')
+ plot(Vc3, 0, 0.03, color='blue')六、拾遗
1、此时此刻(2024年4月19日 16:07),这篇博客才写了一半,发现我在数学计算中用到的相移角似乎有些错误,而且数学计算时的模型和实际电路模型也存在着偏差,所以得到的SageMath结果和仿真结果并不一致。但是二者从数值上看是有相似性和吻合性的,所以应该只是一些小的偏差、错误导致的问题。再假以时日,应该能将相关错误找到,并得出正确的结果。
